Real-life Chess Vision

A computer vision application that identifies pieces on a chess board from real-life photos.
vision
YOLOv8
Roboflow
chess
open cv2
Author

Shai Nisan

Published

March 8, 2023

This post was also published on Roboflow’s blog

Introduction

It all started with a small request from my 8 years old son, who’s a chess player, to make an app that converts images of real-life chess games into a digital format. Then he could save the game for later continuation on his device, share it with friends, or get moves suggestions from chess engines such as Stockfish.

In this post, I’ll go through the journey of building this app.

Understanding the problem

Let’s begin with a clear problem statement: I wanted to take a photo of a real-life chessboard and output a machine-readable format of the board and the pieces on it.

As I’ve quickly found out, chessboard recognition is a popular problem in computer vision, machine learning, and pattern recognition. Throughout the years there have been many works on this topic. The first work that I found was published in 1997(!), and it was fascinating to see how different researchers used their contemporary technologies and algorithms to address this problem since then.

Reading previous work helped me realize that the chess vision problem can be broken down into two main sub-problems:

  1. Chessboard recognition – to identify a chessboard within an image and identify its characteristics: position, orientation, and the location of the squares.

  2. Chess pieces recognition – to detect the pieces on the board, classify them and localize them on the squares.

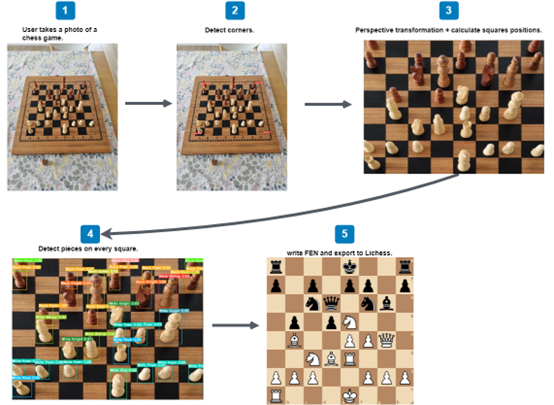
Here’s a sketch of the work process that I needed to figure out:

FEN is the standard notation to describe the positions of a chess game, and computers can also read them.

1. Chessboard recognition

I found three main approaches to chessboard recognition:

  1. Corner-based approaches.
  2. Line-based approaches.
  3. Heatmap approach.

After trying these approaches I’ve found my version of the corners-based approach to work best with real-life images: using YOLOv8 to detect chessboard corners. Once I have the corners’ coordinates, I can start calculating the rest localization of the rest of the board.

To detect the corners, I created a small dataset of about 50 images of chessboards and quickly annotated their corners using Roboflow’s platform. Then I used Roboflow to quickly augment the dataset to X3 its original size and trained a YOLOv8 nano model to detect chessboard corners.

I found that this approach is not affected by different lighting conditions, the capturing angle nor the type of the chessboard, and it was amazing to see how this simple solution outperforms the more sophisticated approaches (at least in my case).

I got great results in detecting corners and could continue to the next phase.

# Load the model.
model = YOLO('yolov8n.pt')

# Training.
 results = model.train(
    data='data.yaml',
    imgsz=640,
    epochs=100,
    batch=8,
    name='yolov8n_corners')

model_trained = YOLO("runs/detect/yolov8n_corners/weights/best.pt")

results = model_trained.predict(source='1.jpgresized.jpg', line_thickness=1, conf=0.25, save_txt=True, save=True)

After detecting the corners, I wanted to rearrange them in a fixed order. I’ve found a small function here that applies simple logic to this problem: the top-left point will have the smallest sum between x and y, whereas the bottom-right point will have the largest sum. The top-right point will have the smallest difference, whereas the bottom-left will have the largest difference.

def order_points(pts):
    
    # order a list of 4 coordinates:
    # 0: top-left,
    # 1: top-right
    # 2: bottom-right,
    # 3: bottom-left
    
    rect = np.zeros((4, 2), dtype = "float32")
    s = pts.sum(axis = 1)
    rect[0] = pts[np.argmin(s)]
    rect[2] = pts[np.argmax(s)]
    
    diff = np.diff(pts, axis = 1)
    rect[1] = pts[np.argmin(diff)]
    rect[3] = pts[np.argmax(diff)]
    
    return rect

Now that I have the coordinates of the four corners of the chessboard in a fixed order, I can compute the perspective transform matrix using OpenCV2.

The perspective transform algorithm transforms the image in a straight manner. This would help calculate the location of all the squares on the chessboard.

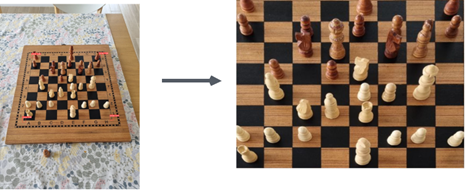
At this stage I can easily calculate the coordinates of all the squares on the board, by simply dividing the upper edge of the image by 8, and then the same for the left edge, and then connecting all the points into lines, to get this:

Each square can then be calculated like that:

a8 = np.array([[xA,y9], [xB, y9], [xB, y8], [xA, y8]])
a7 = np.array([[xA,y8], [xB, y8], [xB, y7], [xA, y7]])
…

Whereas xA, xB, y9, y8, etc. are:

xA = ptsT[0][0]
xB = ptsT[1][0]

y9 = ptsL[0][1]
y8 = ptsL[1][1]
…

Chessboard Squares

2. Chess pieces recognition

Now that I have the coordinates of all the squares on the board, I can go on to classify the chess pieces, and then connect each detection by its coordinates to the corresponding square.

I turned again to YOLOv8 and Roboflow, this time annotating a bigger dataset of chess pieces on chessboards that were transformed using the perspective transform matrix above.

Roboflow makes this stage super-easy, and after 60 minutes or so I had an annotated dataset, that was also augmented automatically by Roboflow, and I could start with training another YOLOv8 model on the chess-pieces detection problem.

YOLOv8 does an excellent job detecting chess pieces! Here’s the correlation matrix:

Now I can connect all the pieces: I have the coordinates of all the squares on the board, and I have the coordinates of the detections on the pieces on the board. Using the “shapely” package, I wrote a simple function that calculates the intersection over union (IoU) between the predicted bounding box and each square on the board.

Then I wrote a function that connects each detection to the correct square – this would be the one that has the largest IoU with the detection’s bounding box. For tall pieces such as the Queen or the King, I considered only the lower half of the bounding box.

def calculate_iou(box_1, box_2):
    poly_1 = Polygon(box_1)
    poly_2 = Polygon(box_2)
    iou = poly_1.intersection(poly_2).area / poly_1.union(poly_2).area
    return iou

At this stage, I could write the FEN of the board with a simple script that orders the connected detections and squares into the correct format and output it to the Lichess FEN URL. With this URL the user can enjoy all the magic that computer chess has to offer - share games, save for later, analyze, get suggestions, etc.

board_FEN = []
corrected_FEN = []
complete_board_FEN = []

for line in FEN_annotation:
    line_to_FEN = []
    for square in line:
        piece_on_square = connect_square_to_detection(detections, square)    
        line_to_FEN.append(piece_on_square)
    corrected_FEN = [i.replace('empty', '1') for i in line_to_FEN]
    print(corrected_FEN)
    board_FEN.append(corrected_FEN)

complete_board_FEN = [''.join(line) for line in board_FEN] 

to_FEN = '/'.join(complete_board_FEN)

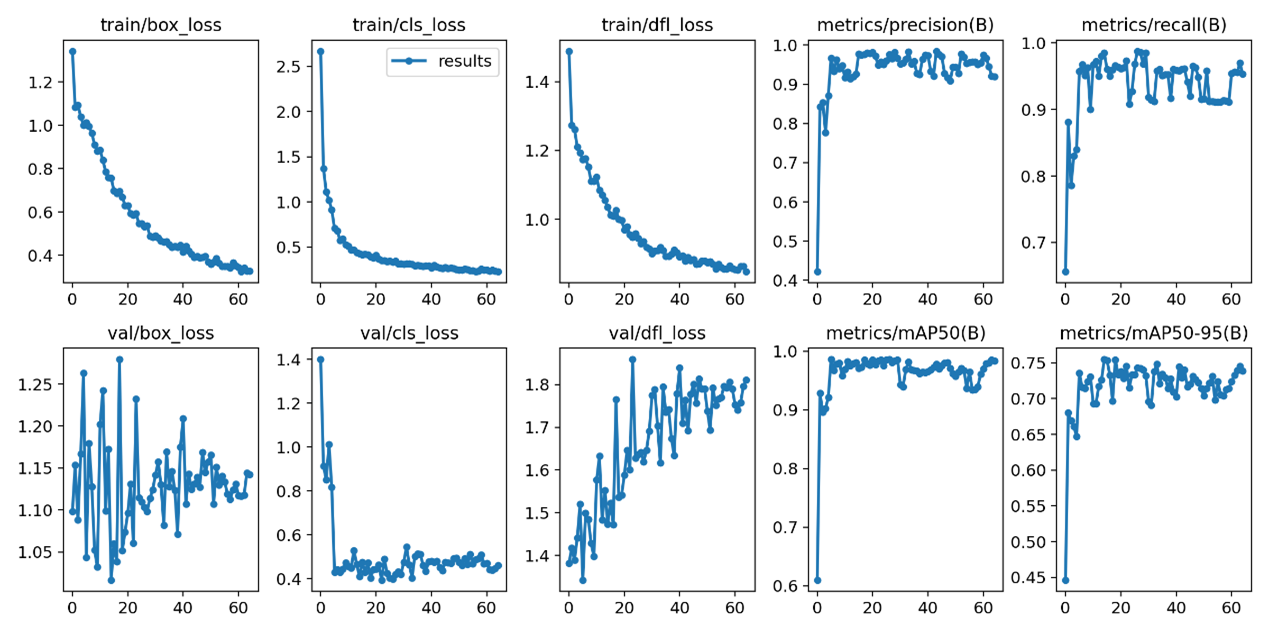
print("https://lichess.org/analysis/"+to_FEN)

The described method performs extremely well and achieves an accuracy of over 99.5% for detecting chessboard corners and 99% for chess piece recognition. This approach is simple, fast, and lightweight while avoiding a time and resource-consuming training process. It can be easily generalized to other kinds of chessboards and chess pieces.

However, the best confirmation of this method’s usefulness is that my son uses it with his friends 😊

The complete process

Here’s a demo of the app:

And that’s me having fun with the Yolo model 😊:

Conclusion

The full code is published on my GitHub.

Please feel free to contact me through LinkedIn with ideas for future iterations of this project.

All the best!